Answer:
The value of x = -1 makes the denominator of the function equal to zero. That is why this value is not included in the domain of f(x)
Explanation:
We have the following expression
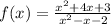
Since the division between zero is not defined then the function f(x) can not include the values of x that make the denominator of the function zero.
Now we search that values of x make 0 the denominator factoring the polynomial

We need two numbers that when adding them get as a result -1 and when multiplying those numbers, obtain -2 as a result.
These numbers are -2 and 1
Then the factors are:
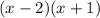
We do the same with the numerator
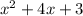
We need two numbers that when adding them get as a result 4 and when multiplying those numbers, obtain 3 as a result.
These numbers are 3 and 1
Then the factors are:

Therefore
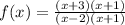
Note that
 only if
only if
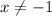
So since
 is not included in the domain the function has a discontinuity in
is not included in the domain the function has a discontinuity in
