Answer: The correct option is (A)

Step-by-step explanation: Given that the sum of two polynomials is
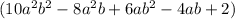 and one addend is
and one addend is
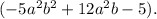
We are to find the other addend.
Let P(x) be the other addend.
Then, according to the given information, we must have
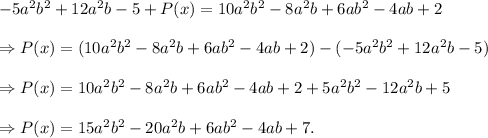
Thus, the other addend is

Option (A) is CORRECT.