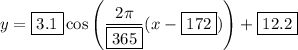We're looking for a model of the form
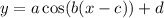
 is the amplitude, equal to half the difference between the maximum and minimum hours of daylight:
is the amplitude, equal to half the difference between the maximum and minimum hours of daylight:
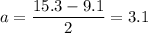
 determines the period of the cosine function. The period itself is
determines the period of the cosine function. The period itself is
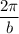 , which we want equal to 365, so that
, which we want equal to 365, so that
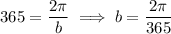
(so that the value in the second box should be 365)
 determines the horizontal shift of the cosine function. We'll come back to this in a moment.
determines the horizontal shift of the cosine function. We'll come back to this in a moment.
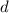 represents the vertical shift of the function. The standard function is bounded between -1 and 1:
represents the vertical shift of the function. The standard function is bounded between -1 and 1:
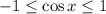
Our new function has an amplitude of 3.1, so that
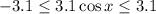
We want the range of values to fall between 15.3 and 9.1, so we want to pick
 such that
such that

So the current model is
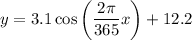
 represents the horizontal shift of the function.
represents the horizontal shift of the function.
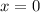 represents the first day of the year, which according to the current model tells us we should expect
represents the first day of the year, which according to the current model tells us we should expect
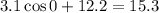 hours of daylight on the first day of the year. But this conflicts with the data. We want this maximum to occur on the 172nd day of the year, so we shift the model by this amount, and the model is
hours of daylight on the first day of the year. But this conflicts with the data. We want this maximum to occur on the 172nd day of the year, so we shift the model by this amount, and the model is