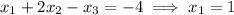Question

Solve this linear system using matrices:

x1 + 2x2 − x3 = −4
x1 + 2x2 + x3 = 2
−x1 − x2 + 2x3 = 6

Answer 1

1

-1

3

Explanation:

j did it on edge

Answer 2

In matrix form, the system is

`\begin{bmatrix}1&2&-1\\1&2&1\\-1&-1&2\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}-4\\2\\6\end{bmatrix}`

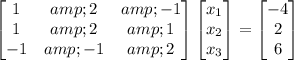
Solving this "using matrices" is a bit ambiguous but brings to mind two standard methods.

• Using inverses:

Compute the inverse of the coefficient matrix using the formula

`\mathbf A^(-1)=\frac1{\det\mathbf A}\mathbf C^\top`

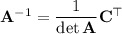
where
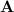`\mathbf A` is the coefficient matrix,
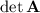`\det\mathbf A` is its determinant,
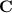`\mathbf C` is the cofactor matrix, and
`\top` denotes the matrix transpose.

We compute the determinant by a Laplace expansion along the first column:

`\det\mathbf A=\begin{vmatrix}1&2&-1\\1&2&1\\-1&-1&2\end{vmatrix}`

`\det\mathbf A=\begin{vmatrix}2&1\\-1&2\end{vmatrix}-\begin{vmatrix}2&-1\\-1&2\end{vmatrix}-\begin{vmatrix}2&-1\\2&1\end{vmatrix}`

`\det\mathbf A=5-3-4=-2`

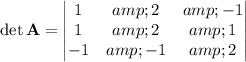
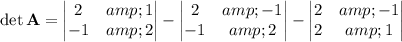
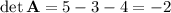
The cofactor matrix is

`\mathbf C=\begin{bmatrix}5&-3&1\\-3&1&-1\\4&-2&0\end{bmatrix}\implies\mathbf C^\top=\begin{bmatrix}5&-3&4\\-3&1&-2\\1&-1&0\end{bmatrix}`

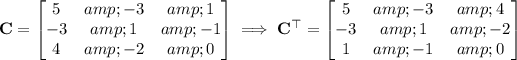
which makes the inverse

`\mathbf A^(-1)=\begin{bmatrix}-5/2&3/2&-2\\3/2&-1/2&1\\-1/2&1/2&0\end{bmatrix}`

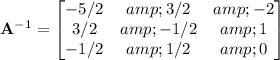
Finally,

`\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\mathbf A^(-1)\begin{bmatrix}-4\\2\\6\end{bmatrix}\implies\boxed{x_1=1,x_2=-1,x_3=3}`

• Gauss-Jordan elimination:

Take the augmented matrix

`\begin{bmatrix}1&2&-1&-4\\1&2&1&2\\-1&-1&2&6\end{bmatrix}`

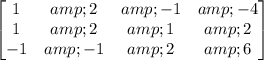
Subtract row 1 from row 2, and -(row 1) from row 3:

`\begin{bmatrix}1&2&-1&-4\\0&0&2&6\\0&1&1&2\end{bmatrix}`

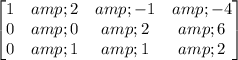
Multiply row 2 by 1/2:

`\begin{bmatrix}1&2&-1&-4\\0&0&1&3\\0&1&1&2\end{bmatrix}`

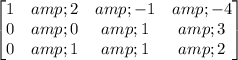
The second row tells us that

`x_3=3`

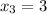
Then in the third row,

`x_2+x_3=2\implies x_2=-1`

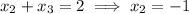
Then in the first row,

`x_1+2x_2-x_3=-4\implies x_1=1`