Question

What is the slope of a line perpendicular to the line whose equation is y = 2x+5?

slope = -1
slope =
slope = -2

Answer 1

slope = -
`(1)/(2)`

Explanation:

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

y = 2x + 5 is in this form with slope m = 2

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(2)`

Answer 2

Slope
`m_(2) = (-1)/(2)`.

Explanation:

Given : equation is y = 2x+5.

To find : What is the slope of a line perpendicular to the line.

Solution : We have given y = 2x+5.

On comparing by the slope form of line is

y = mx + b

where, m = slope , b = y-inercept.

So ,
`m_(1)` = 2 .

When the two line are perpendicular to each other then thier slope is

`m_(2) = (-1)/(m_(1))`.

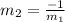Then plug the value of
`m_(1)` = 2 .

`m_(2) = (-1)/(2)`.

`m_(2) = (-1)/(2)`.

Therefore, Slope
`m_(2) = (-1)/(2)`.