Question

What are the domain and range of the function f(x)=-square root x+3-2?

Answer 1

The answer for this equation is C.

Answer 2

For this case we have the following function:

`f (x) = - \sqrt {x + 3} -2`

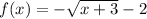
By definition, the domain is given by all the values for which the function is defined.

The given function is no longer defined if the argument of the root is negative. So:

`x + 3 \geq0\\x \geq-3`

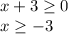
Thus, the domain of the function is given by all the values of x greater than or equal to -3.

Domain: [-3, ∞)

Substituting the values of the domain, we find the range.

`f (-3) = - \sqrt {-3 + 3} -2 = -2`

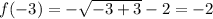
The function evaluated in ∞ gives -∞. So the range is given by:

(-∞, 2]

Answer:

Domain: [-3, ∞)

Range: (-∞, 2]