Question

What is an extraneous solution to a radical equation

Answer 1

A solution of the radical equation that does not satisfy the original radical equation.

Step-by-step explanation

An extraneous is the solution that does not satisfy the original equation.

For instance, given the radical equation:

`√(x + 3) = x - 3`

We square both sides to get:

`{ (√(x + 3) )}^(2) = {(x - 3)}^(2)`

We expand to get;

`{x + 3} = {x}^(2) - 6x + 9`

We write in standard quadratic forms:

`{x}^(2) - 6x - x + 9 - 3= 0`

`{x}^(2) - 7x+6= 0`

`{(x - 6)(x - 1)} = 0`

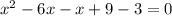
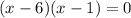
This implies that;

`x = 1 \: or \: x = 6`

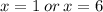
When we substitute x= 6 into the equation, we get;

`√(6+ 3) = 6- 3`

`√(9) = 3`

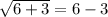
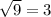
This statement is true.

However when we substitute x=1, we get:

`√(1+ 3) = 1- 3`

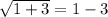
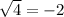`√(4) = - 2`This statement is false.

Hence x=1 u s referred to as an extraneous solution.