Question

The population of a small town is decreasing exponentially at a rate of 14.3% each year. The current population is 9,400 people. The town's tax status will change once the population is below 6,000 people. Create an inequality that can be used to determine after how many years, t, the town's tax status will change, and use it to answer the question below.

Answer 1

After 2.9 years the town's tax status will change

The towns tax status change within the next 3 years

Explanation:

The question below is

Will the towns tax status change within the next 3 years ?

Let

y -----> the population of a small town

t ----> the number of years

we have a exponential function of the form

`y=a(b)^(t)`

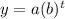
where

a is the initial value

b is the base

In this problem

`a=9,400\ people`

`b=100\%-14.3\%=85.7\%=85.7/100=0.857`

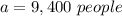
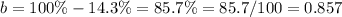
substitute

`y=9,400(0.857)^(t)`

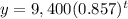
Remember that

The town's tax status will change once the population is below 6,000 people

so

The inequality that represent this situation is

`9,400(0.857)^(t)< 6,000`

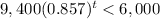
Solve for t

`(0.857)^(t)< 6,000/9,400`

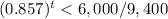
Apply log both sides

`(t)log(0.857)< log(6,000/9,400)`

`-0.067t< -0.1950`

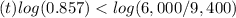
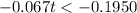
Multiply by -1 both sides

`0.067t > 0.1950`

`t > 2.9\ years`

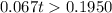
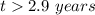
so

After 2.9 years the town's tax status will change

therefore

The answer is

Yes, the towns tax status change within the next 3 years