Answer:
The domain is all real numbers. The range is y
Explanation:
we have
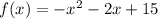
This is the equation of a vertical parabola open downward
The vertex is a maximum
Find the vertex of the quadratic equation
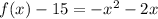
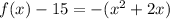
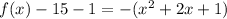
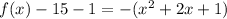
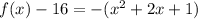
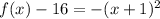
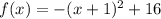 -----> equation in vertex form
-----> equation in vertex form
The vertex is the point (-1,16)
therefore
The domain is the interval ----> (-∞,∞) All real numbers
The range is the interval ----> (-∞,16] All real numbers less than or equal to 16