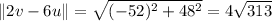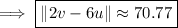Question

Help Me! I suck with vectors.
Look at the attached pictures for the problem.

Answer 1

Multiplying a vector
`x` by a constant
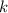`k` gives you a new vector whose components are the same as
`x`, but scaled by
`k`:

`x=\langle x_1,x_2\rangle\implies x=\langle kx_1,kx_2\rangle`

So we have

`u=\langle5,-7\rangle\implies-6u=\langle-30,42\rangle`

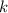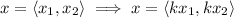
`v=\langle-11,3\rangle\implies2v=\langle-22,6\rangle`

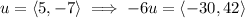
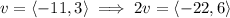
Vector addition is just a matter of adding the corresponding components together:

`x=\langle x_1,x_2\rangle,y=\langle y_1,y_2\rangle\implies x+y=\langle x_1+y_1,x_2+y_2\rangle`

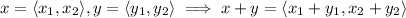
Then

`2v-6u=\langle-22,6\rangle+\langle-30,42\rangle=\langle-22-30,6+42\rangle`

`\implies\boxed{2v-6u=\langle-52,48\rangle}`

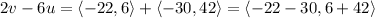
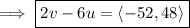
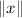`\|x\|` denotes the norm/magnitude of the vector
`x`:

`x=\langle x_1,x_2\rangle\implies\|x\|=\sqrt{{x_1}^2+{x_2}^2}`

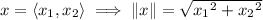
We have

`\|2v-6u\|=√((-52)^2+48^2)=4√(313)`

`\implies\boxed\`