Question

DO NOT ANSWER W/O EXPLANATION PLEASE! NEED WRITTEN SOLUTION.

In triangle ABC, an altitude is drawn from vertex C to the line containing AB. The length of this altitude is h and h=AB. Which of the following is true?
I. Triangle ABC could be a right triangle.
II. Angle C cannot be a right angle.
III. Angle C could be less than 45 degrees.

Answer 1

We have altitude h to side AB and AB=h, i.e. the altitude is congruent to the side it goes to.

That's all kinds of triangles. One way to see them is using two horizontal parallel lines h apart, the bottom one with a base AB=h somewhere on it. Then any C on the top line makes a triangle ABC with altitude h=AB.

Let's go through the choices.

I. ABC could be a right triangle. That's TRUE.

We could have the isoscleles right triangle, C directly above B, so AC is the leg and an altitude, AB=AC and B is the right angle.

II. Angle C cannot be a right angle. That's TRUE.

The biggest angle C can be is when it's over the midpoint of AB, so if AB=2, h=2, and

`AC=√(2^2+1^2)=√(5)`

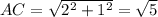
so

`C_{\textrm{max}} = 2 \arctan(1/2) \approx 53.13^\circ`

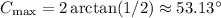
III. Angle C could be less than 45 degrees. That's TRUE.

As long as C stays on our top parallel, we can make it as acute as we like by going farther away from AB.

All true. Hmmm.