Question

In sodium chloride, the distance between the center of the sodium ion and the centerof an adjacent chloride ion is 2.819 angstroms. Calculate the density in g/cm3of an ideal NaCl crystal from this information and what you learned from this lab.Hints: To calculate mass, determine how many equivalent ions are in a unit cell. To determinevolume of the unit cell, start by determining the length of on side of the unit cell.

Answer 1

`\boxed{\text{2.17 g/cm}^(3)}`

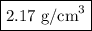
Step-by-step explanation:

1. Ions per unit cell

(a) Chloride

8 corners + 6 faces

`\text{No. of Cl$^(-)$ ions}\\\\= \text{8 corners} * \frac{(1 )/( 8) \text{ ion}} {\text{1 corner}} + \text{6 faces}* \frac{(1)/(2) \text{ ion}}{\text{1 face}} = \text{1 ion + 3 ions = 4 ions}}`

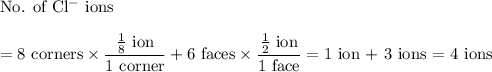
(b) Chloride

12 edges + 1 centre

`\text{No. of Na$^(+)$ ions}\\\\= \text{12 edges} * \frac{(1 )/( 4) \text{ ion}} {\text{1 edge}} + \text{1 centre}*\frac{\text{1 ion}}{\text{1 centre}} = \text{3 ions + 1 ion = 4 ions}`

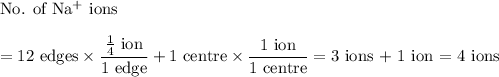
There are four formula units of NaCl in a unit cell.

2. Mass of unit cell

m = 4 × NaCl = 4 × 58.44 u = 233.76 u

`m = \text{233.76 g} * \frac{\text{1 g} }{6.022 * 10^(23) \text{ u} } = 3.882 * 10^(-22)\text{ g}`

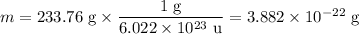
3. Volume of unit cell

(a) Edge length

`a = 2d_{\text{Na-Cl}} = 2 * \text{2.819 \AA} = 5.638 *10^(-10) \text{ m} = 5.638 *10^(-8) \text{ cm}`

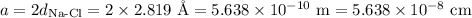
(b) Volume

`V = a^(3) = \left( 5.638 * (10^(-8) \text{ cm}\right)^(3) = 1.792 *10^(-22) \text{ cm}^(3)`

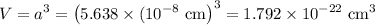
4. Density

`\rho = \frac{\text{mass}}{\text{volume}} = \frac{3.882 * 10^(-22)\text{ g}}{1.792 *10^(-22) \text{ cm}^(3)}} = \text{2.17 g/cm}^(3)\\\\\text{The density of NaCl is }\boxed{\textbf{2.17 g/cm}^(3)}`