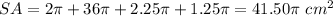Question

A jumbo crayon is composed of a cylinder with a conical tip. The cylinder is 12 cm tall with a radius of 1.5 cm, and the cone has a slant height of 2 cm and a radius of 1 cm. The lateral area of the cone is π cm2. To wrap paper around the entire lateral surface of the cylinder, π cm2 of paper is needed. The surface area, including the bottom base of the crayon, is π cm2.

Answer 1

2

36

41.5

Explanation:

just got it all right even though I guessed soooo, yay

Explanation:

Answer 2

Part 1) The lateral area of the cone is
`LA=2\pi\ cm^(2)`

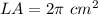
Part 2) The lateral surface area of the cylinder is
`LA=36\pi\ cm^(2)`

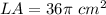
Part 3) The surface area of the crayon is
`SA=41.50\pi\ cm^(2)`

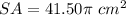
Explanation:

Part 1) Find the lateral area of the cone

The lateral area of the cone is equal to

`LA=\pi rl`

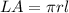
we have

`r=1\ cm`

`l=2\ cm`

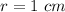
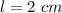
substitute

`LA=\pi (1)(2)`

`LA=2\pi\ cm^(2)`

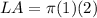
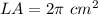
Part 2) Find the lateral surface area of the cylinder

The lateral area of the cylinder is equal to

`LA=2\pi rh`

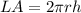
we have

`r=1.5\ cm`

`h=12\ cm`

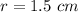
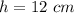
substitute

`LA=2\pi (1.5)(12)`

`LA=36\pi\ cm^(2)`

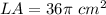
Part 3) Find the surface area of the crayon

The surface area of the crayon is equal to the lateral area of the cone, plus the lateral area of the cylinder, plus the top area of the cylinder plus the bottom base of the crayon

Find the area of the bottom base of the crayon

`A=\pi[r2^(2)-r1^(2)]`

where

r2 is the radius of the cylinder

r1 is the radius of the cone

substitute

`A=\pi[1.5^(2)-1^(2)]`

`A=1.25\pi\ cm^(2)`

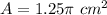
Find the area of the top base of the cylinder

`A=\pi(1.5)^(2)=2.25\pi\ cm^(2)`

Find the surface area

`SA=2\pi+36\pi+2.25\pi+1.25\pi=41.50\pi\ cm^(2)`