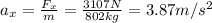Question

On an airplane's takeoff, the combined action of the air around the engines and wings of an airplane exerts a 8420-N force on the plane, directed upward at an angle of 69.0° above the horizontal. The plane rises with constant velocity in the vertical direction while continuing to accelerate in the horizontal direction. (a) What is the weight of the plane? N (b) What is its horizontal acceleration?

Answer 1

(a) 7861 N

Along the vertical direction, the plane is moving at constant velocity: this means that the net vertical acceleration is zero, so the vertical component of the 8420 N upward force is balanced by the weight (pointing downward).

The vertical component of the upward force is given by:

`F_y = F sin \theta`

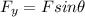
where

F = 8420 N is the magnitude of the force

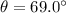`\theta=69.0^(\circ)` is the angle above the horizontal

Substituting,

`F_y = (8420 N)(sin 69.0^(\circ)) =7861 N`

This means that the weight of the plane is also 7861 N.

(b) 3.87 m/s^2

From the weight of the plane, we can calculate its mass:

`m=(W)/(g)=(7861 N)/(9.8 m/s^2)=802 kg`

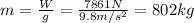
Where g = 9.8 m/s^2 is the acceleration due to gravity.

Along the horizontal direction, the 8420 N is not balanced by any other backward force: so, there is a net acceleration along this direction.

The horizontal component of the force is given by

`F_x = F cos \theta = (8420 N)(cos 69.0^(\circ))=3107 N`

According to Newton's second law, the net force along the horizontal direction is equal to the product between the plane's mass and the horizontal acceleration:

`F_x = m a_x`

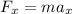
so if we solve for a_x, we find:

`a_x = (F_x)/(m)=(3107 N)/(802 kg)=3.87 m/s^2`