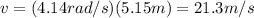Question

Human centrifuges are used to train military pilots and astronauts in preparation for high-g maneuvers. A trained, fit person wearing a g-suit can withstand accelerations up to about 9g (88.2 m/s2) without losing consciousness. HINT (a) If a human centrifuge has a radius of 5.15 m, what angular speed (in rad/s) results in a centripetal acceleration of 9g? rad/s (b) What linear speed (in m/s) would a person in the centrifuge have at this acceleration? m/s

Answer 1

Step-by-step explanation:

(a) Centripetal acceleration,
`a=9g=88.2\ m/s^2`

Radius, r = 5.15 m

Let
`\omega` is the angular speed. The relation between the angular speed and angular acceleration is given by :

`a=\omega^2 r`

`\omega=\sqrt{(a)/(r)}`

`\omega=\sqrt{(88.2)/(5.15)}`

`\omega=4.13\ rad/s`

(b) Let v is the linear speed of the person in the centrifuge have at this acceleration. It is given by :

`v=r* \omega`

`v=5.15* 4.13`

v = 21.26 m/s

Hence, this is the required solution.

Answer 2

(a)
`4.14 rad/s^2`

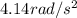
The relationship beween centripetal acceleration and angular speed is

`a=\omega^2 r`

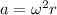
where

`\omega` is the angular speed

r is the radius of the circular path

Here we gave

`a = 9g = 88.2 m/s^2` is the centripetal acceleration

r = 5.15 m is the radius

Solving for
`\omega`, we find:

`\omega = \sqrt{(a)/(r)}=\sqrt{(88.2 m/s^2)/(5.15 m)}=4.14 rad/s^2`

(b) 21.3 m/s

The relationship between the linear speed and the angular speed is

`v=\omega r`

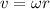
where

v is the linear speed

`\omega` is the angular speed

r is the radius of the circular path

In this problem we have

`\omega=4.14 rad/s`

r = 5.15 m

Solving the equation for v, we find

`v=(4.14 rad/s)(5.15 m)=21.3 m/s`