Answer:
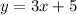
Explanation:
First, find the rate of change [slope]:
-y₁ + y₂\-x₁ + x₂ = m
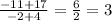
Now, plug the coordinates into the Slope-Intercept Formula instead of the Point-Slope Formula because you get it done much swiftly. It does not matter which ordered pair you choose:
17 = 3[4] + b
12
5 = b
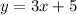
__________________________________________________________
11 = 3[2] + b
6
5 = b
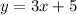
You see? I told you it did not matter which ordered pair you choose because you will always get the exact same result.
I am joyous to assist you anytime.