For this case we propose a system of equations:
x: Variable representing the weight of large boxes
y: Variable that represents the weight of the small boxes
So
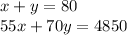
We clear x from the first equation:
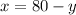
We substitute in the second equation:
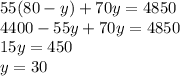
We look for the value of x:
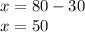
Large boxes weigh 50 pounds and small boxes weigh 30 pounds
Answer:
Large boxes weigh 50 pounds and small boxes weigh 30 pounds