Question

You roll two fair dice, a green one and a red one.

Required:
a. What is the probability of getting a sum of 8? (Enter your answer as a fraction.)
b. What is the probability of getting a sum of 4?
c. What is the probability of getting a sum of 8 or 4?
d. Are these outcomes mutually exclusive?

Answer 1

`a.\ (5)/(36)\\b.\ (1)/(12)\\c.\ (2)/(9)\\d.\ $Not mutually exclusive$`

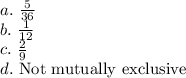
Explanation:

Given two fair dice are rolled, one green and one red.

To find:

a. Probability of getting a sum of 8.

b. Probability of getting a sum of 4.

c. Probability of getting a sum of 8 or 4.

d. Are these outcomes mutually exclusive?

Solution:

First of all, let us have a look at the output of roll of two dice.

There are a total of 36 outcomes.

{(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)}

a. Getting a sum equal to 8, we have following outcomes:

{(2, 6), (3,5), (4, 4), (5,3), (6, 2)}

5 possible outcomes for this event.

Formula for probability of an event E can be observed as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

`P($Getting 8$) = (5)/(36)`

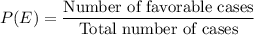
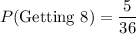
b. Getting a sum equal to 4, we have following outcomes:

{(1, 3), (2,2), (3, 1)}

3 possible outcomes for this event.

Formula for probability of an event E can be observed as:

`P($Getting 4$) = (3)/(36) = (1)/(12)`

c. Probability of getting a sum of 8 or 4?

Following possible outcomes are there:

{(2, 6), (3,5), (4, 4), (5,3), (6, 2), (1, 3), (2,2), (3, 1)}

Total 8 possible outcomes:

`P($Getting 8 or 4$) = (8)/(36) = (2)/(9)`

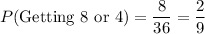
d. Are these outcomes mutually exclusive?

These events are not mutually exclusive because they contain the similar outcome from both of the dice.

i.e. (4, 4) and (2, 2)