Answer: The correct option is
(A)
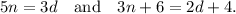
Step-by-step explanation: Given that the numerator and denominator of a fraction are in the ratio of 3 to 5. When the numerator and denominator are both increased by 2, the fraction is equal to \dfrac{2}{3}.
We are to select the system of equations that could be used to solve the problem.
Since n denotes the numerator and m denotes the denominator of the given fraction, so we have

and
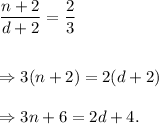
Thus, the required system of equations is
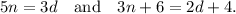
Option (A) is CORRECT.