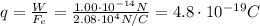Question

Millikan measured the electron's charge by observing tiny charged oil drops in an electric field. Each drop had a charge imbalance of only a few electrons. The strength of the electric field was adjusted so that the electric and gravitational forces on a drop would balance and the drop would be suspended in air. In this way the charge on the drop could be calculated. The charge was always found to be a small multiple of 1.60 × 10-19 C. Find the charge on an oil drop weighing 1.00 × 10-14 N and suspended in a downward field of magnitude 2.08 × 104 N/C.

Answer 1

`4.8\cdot 10^(-19) C`

Step-by-step explanation:

For a drop in equilibrium, the weight is equal to the electric force (in magnitude):

`W = F_e`

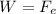
where here we have

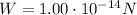`W=1.00\cdot 10^(-14)N` is the weight of the drop

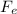`F_e` is the magnitude of the electric force, which can be rewritten as

`F_e = qE`

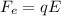
where

q is the charge of the oil drop

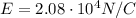`E=2.08 \cdot 10^4 N/C` is the magnitude of the electric field

Substituting into the equation and solving for q, we find the charge of the oil drop:

`q=(W)/(F_e)=(1.00\cdot 10^(-14)N)/(2.08\cdot 10^4 N/C)=4.8\cdot 10^(-19) C`