Answer: (-a-b, c)
Explanation:
We know that the mid point of a line having endpoints
 and
and
 is given by :-
is given by :-
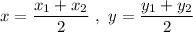
In the given figure it can be seen that D is the midpoint of RT :
Since R(-2b , 2c) and T(-2a, 0)
Then , the midpoint D of a line having endpoints
 and
and
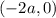 is given by :-
is given by :-

Hence , the coordinates of midpoint D = (-a-b, c)