Answer:
 and w= 21 inches.
and w= 21 inches.
Explanation:
The placemat has an area of
 . Now, let's call w to the width, the exercise says that the length of the placemat is four times the quantity of nine less than half its width, that is
. Now, let's call w to the width, the exercise says that the length of the placemat is four times the quantity of nine less than half its width, that is
length = 4(w/2-9).
Now, the area is length*width, so
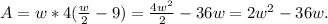
and we know that
 , so
, so
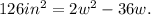
Now, let's find the solution.
 is a quadratic formula of the form
is a quadratic formula of the form
 with a=2, b= -36 and c = -126. The solutions will be
with a=2, b= -36 and c = -126. The solutions will be


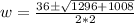
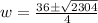

 or
or

 or
or
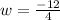
as we are searching a distnace, we are going to use the positive solution, that is
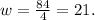
Then, the width is 21 inches.