Question

Using Cramer's Rule, what is the value of x in the system of linear equations below?

3x + 4y = 12
x-6y=-18

Answer 1

A on Edg ^

took the test

Answer 2

0

Explanation:

We find the determinant of a matrix by the method below. If we have a matrix:

`\left[\begin{array}{cc}a&b\\c&d\end{array}\right]`

The determinant is
`ad-bc`

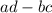
Now, using cramer's rule, we find x-value by the formula:

`x=(D_x)/(D)`

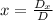
Where D is the determinant of the original problem and
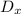`D_x` is the determinant of the x-value matrix. How do we get those?

To get original matrix and thus D, we set up the matrix as the coefficients of x and y (s) of both the equations and to get matrix of x-value and thus
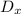`D_x`, we replace the x values of the matrix with the numbers in the right hand side of the 2 equations. We show this below:

To get D:

`\left[\begin{array}{cc}3&4\\1&-6\end{array}\right] \\D=(3)(-6)-(1)(4)=-18-4=-22`

To get
`D_x`:

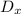`\left[\begin{array}{cc}12&4\\-18&-6\end{array}\right] \\D_x=(12)(-6)-(-18)(4)=0`

Putting into the formula, we get:

`x=(D_x)/(D)=(0)/(-22)=0`

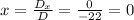
Thus, the value of x is 0