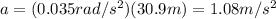(a) 24.6 Nm
The torque produced by the net thrust about the center of the circle is given by:
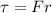
where
F is the magnitude of the thrust
r is the radius of the wire
Here we have
F = 0.795 N
r = 30.9 m
Therefore, the torque produced is

(b)

The equivalent of Newton's second law for a rotational motion is
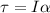
where
 is the torque
is the torque
I is the moment of inertia
 is the angular acceleration
is the angular acceleration
If we consider the airplane as a point mass with mass m = 0.741 kg, then its moment of inertia is
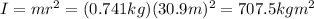
And so we can solve the previous equation to find the angular acceleration:
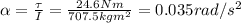
(c)
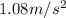
The linear acceleration (tangential acceleration) in a rotational motion is given by
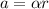
where in this problem we have
 is the angular acceleration
is the angular acceleration
r = 30.9 m is the radius
Substituting the values, we find