2Ω. Based on the graph the resistance of the bulb is 2Ω.
Based on the graph of the image we can see there are a linear proportionality between the voltage and the current. So, we can modeling this problem calculating the slope of the straight line in the graph as follow:
We can write a formula of the form
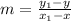 .
.
From the Ohm's Law we know that the resistance is directly proportional to the voltage and inversely proportional to the current
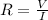 .
.
From the graph we can see in the x-axis the values of the voltage and the y-axis the value of the current, with the points (x, y) = (2, 1) and (x₁, y₁) = (4, 2) marked in the graph, we can write:
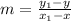
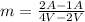
We need to express the equation
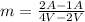 in the form
in the form
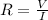 :
:
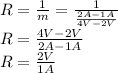
R = 2Ω