Question

A 60-W, 120-V light bulb and a 200-W, 120-V light bulb are connected in series across a 240-V line. Assume that the resistance of each bulb does not vary with current. (Note: This description of a light bulb gives the power it dissipates when connected to the stated potential difference; that is, a 25-W, 120-V light bulb dissipates 25 W when connected to a 120-V line.) A. Find the current through the bulbs. B. Find the power dissipated in the 60 W bulb. C. Find the power dissipated in the 200 W bulb. D. One bulb burns out very quickly. Which one? 60-W bulb, 200-W bulb.

Answer 1

A. 0.77 A

Using the relationship:

`P=(V^2)/(R)`

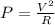
where P is the power, V is the voltage, and R the resistance, we can find the resistance of each bulb.

For the first light bulb, P = 60 W and V = 120 V, so the resistance is

`R_1=(V^2)/(P)=((120 V)^2)/(60 W)=240 \Omega`

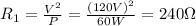
For the second light bulb, P = 200 W and V = 120 V, so the resistance is

`R_1=(V^2)/(P)=((120 V)^2)/(200 W)=72 \Omega`

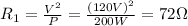
The two light bulbs are connected in series, so their equivalent resistance is

`R=R_1 + R_2 = 240 \Omega + 72 \Omega =312 \Omega`

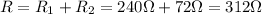
The two light bulbs are connected to a voltage of

V = 240 V

So we can find the current through the two bulbs by using Ohm's law:

`I=(V)/(R)=(240 V)/(312 \Omega)=0.77 A`

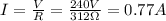
B. 142.3 W

The power dissipated in the first bulb is given by:

`P_1=I^2 R_1`

where

I = 0.77 A is the current

`R_1 = 240 \Omega` is the resistance of the bulb

Substituting numbers, we get

`P_1 = (0.77 A)^2 (240 \Omega)=142.3 W`

C. 42.7 W

The power dissipated in the second bulb is given by:

`P_2=I^2 R_2`

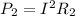
where

I = 0.77 A is the current

`R_2 = 72 \Omega` is the resistance of the bulb

Substituting numbers, we get

`P_2 = (0.77 A)^2 (72 \Omega)=42.7 W`

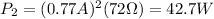
D. The 60-W bulb burns out very quickly

The power dissipated by the resistance of each light bulb is equal to:

`P=(E)/(t)`

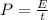
where

E is the amount of energy dissipated

t is the time interval

From part B and C we see that the 60 W bulb dissipates more power (142.3 W) than the 200-W bulb (42.7 W). This means that the first bulb dissipates energy faster than the second bulb, so it also burns out faster.