Question

A particle's position is given by x = 7.00 - 9.00t + 3t2, in which x is in meters and t is in seconds. (a) What is its velocity at t = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed increasing or decreasing just then? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? If so, give the time t; if not, answer "0". (f) Is there a time after t = 3 s when the particle is moving in the negative direction of x? If so, give the time t; if not, answer "0".

Answer 1

`x(t)=7.00\,\mathrm m-\left(9.00(\rm m)/(\rm s)\right)t+\left(3(\rm m)/(\mathrm s^2)\right)t^2`

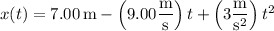
a. The particle has velocity at time
`t`,

`(\mathrm dx(t))/(\mathrm dt)=-9.00(\rm m)/(\rm s)+\left(6(\rm m)/(\mathrm s^2)\right)t`

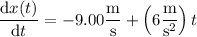
so that after
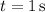`t=1\,\mathrm s` it will have velocity
`\boxed{-3.00(\rm m)/(\rm s)}`.

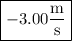b. The sign of the velocity is negative, so it's moving in the negative
`x` direction.

c. Its speed is 3.00 m/s.

d. The particle's velocity changes according to

`(\mathrm d^2x(t))/(\mathrm dt^2)=6(\rm m)/(\mathrm s^2)`

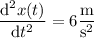
which is positive and indicates the velocity/speed of the particle is increasing.

e. Yes. The velocity is increasing at a constant rate. Solving for
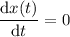`(\mathrm dx(t))/(\mathrm dt)=0` is trivial; this happens when
`\boxed{t=1.50\,\mathrm s}`.

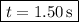f. No, the velocity is positive for all
`t` beyond 1.50 s.