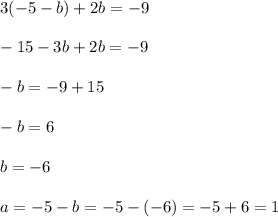Question

8. Suppose the curve y = x4 + ax3 + bx2 + cx + d has a tangent line when

x = 0 with equation y = 2x + 1, and a tangent line when x = 1 with equation
y= 2 – 3x. Find the values of a, b, c and d.

Answer 1

a=1, b=-6, c=2, d=1

Explanation:

You are given the function

`y=x^4+ax^3+bx^2+cx+d`

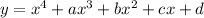
Find the derivative:

`y'=4x^3+3ax^2+2bx+c`

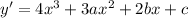
The curve has a tangent line when x = 0 with equation y = 2x + 1, so

`y'(0)=2\\ \\y(0)=1`

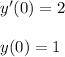
Hence,

`y'(0)=4\cdot 0^3+3a\cdot 0^2+2b\cdot 0+c=2\Rightarrow c=2\\ \\y(0)=0^4+a\cdot 0^3+b\cdot 0^2+2\cdot 0+d=1\Rightarrow d=1`

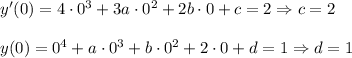
The curve has a tangent line when x = 1 with equation y = -3x + 2, so

`y'(1)=-3\\ \\y(1)=-3+2=-1`

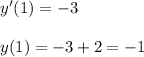
So,

`y'(1)=4\cdot 1^3+3a\cdot 1^2+2b\cdot 1+c=4+3a+2b+2=-3\Rightarrow 3a+2b=-9\\ \\y(1)=1^4+a\cdot 1^3+b\cdot 1^2+2\cdot 1+d=1+a+b+2+1=-1\Rightarrow a+b=-5`

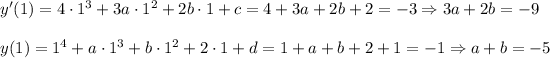
From the second equation, a=-5-b, substitute it into the first one:

`3(-5-b)+2b=-9\\ \\-15-3b+2b=-9\\ \\-b=-9+15\\ \\-b=6\\ \\b=-6\\ \\a=-5-b=-5-(-6)=-5+6=1`