Answer:
dy/dx =
![(1)/((4x^(3)-7))*[((3x^(5)+1)(12x^(2))-(4x^(3)-7)(15x^(4)))/((3x^(5)+1))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qul08ck9lvh17d01pq5bns5b7dxi68gor8.png)
Explanation:
* Lets revise some rules for the derivative
- The derivative of ㏑(f(x)) = 1/f(x) × f'(x)
- The derivative of u/v = (vu'-uv')/v²
- The derivative of the constant is 0
* Lets solve the problem
∵ y = ㏑[(4x³ - 7)/(3x^5 + 1)]
- Let u = 4x³ - 7 and v = 3x^5 + 1
∵ u = 4x³ - 7
∴ u' = 4(3)x^(3-1) - 0 = 12x²
∵ v = 3x^5 + 1
∴ v' = 3(5)x^(5-1) + 0 = 15x^4
∵ The derivative of u/v = (vu' - uv')/v²
∴ The derivative of u/v =
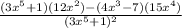
∵ The derivative of ㏑(f(x)) = 1/f(x) × f'(x)
∴ dy/dx =
![(1)/(((4x^(3)-7))/((3x^(5)+1)))*[((3x^(5)+1)(12x^(2))-(4x^(3)-7)(15x^(4))/((3x^(5)+1)^(2))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/anjljhi2x7lnbp9dj5t9x01dmjh79gj7w4.png)
- Simplify by cancel bracket (3x^5 + 1)from the 1st fraction with the
same bracket in the 2nd fraction
∴ dy/dx =
![(1)/((4x^(3)-7))*[((3x^(5)+1)(12x^(2))-(4x^(3)-7)(15x^(4)))/((3x^(5)+1))]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qul08ck9lvh17d01pq5bns5b7dxi68gor8.png)