Answer:
The correct answer option is C. 56.
Explanation:
We are given that a group of 8 friends (5 girls and 3 boys) plans to watch a movie, but they have only 5 tickets.
We are to find the number of combinations these 5 friends could
possibly receive the tickets.
Here, we will use the concept of combination as the order of the friends is not specific.
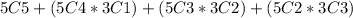
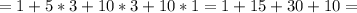 56
56