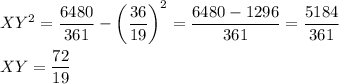Question

Triangle $ABC$ has side lengths $AB = 9$, $AC = 10$, and $BC = 17$. Let $X$ be the intersection of the angle bisector of $\angle A$ with side $\overline{BC}$, and let $Y$ be the foot of the perpendicular from $X$ to side $\overline{AC}$. Compute the length of $\overline{XY}$.

Answer 1

`(72)/(19)`

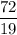
Explanation:

Consider triangle ABC. Segment AX is angle A bisector. Its length can be calculated using formula

`AX^2=(AB\cdot AC)/((AB+AC)^2)\cdot ((AB+AC)^2-BC^2)`

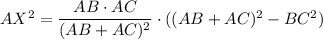
Hence,

`AX^2=(9\cdot 10)/((9+10)^2)\cdot ((9+10)^2-17^2)=(90)/(361)\cdot (361-289)=(90)/(361)\cdot 72=(6480)/(361)`

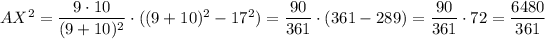
By the angle bisector theorem,

`(AB)/(AC)=(BX)/(XC)`

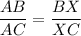
So,

`(9)/(10)=(BX)/(17-BX)\Rightarrow 153-9BX=10BX\\ \\19BX=153\\ \\BX=(153)/(19)`

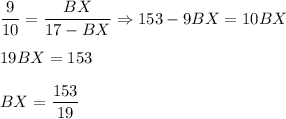
and

`XC=17-(153)/(19)=(170)/(19)`

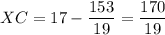
By the Pythagorean theorem for the right triangles AXY and CXY:

`AX^2=AY^2+XY^2\\ \\XC^2=XY^2+CY^2`

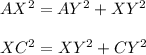
Thus,

`(6480)/(361)=XY^2+AY^2\\ \\\left((170)/(19)\right)^2=XY^2+(10-AY)^2`

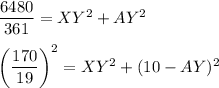
Subtract from the second equation the first one:

`(28900)/(361)-(6480)/(361)=(10-AY)^2-AY^2\\ \\(22420)/(361)=100-20AY+AY^2-AY^2\\ \\(1180)/(19)=100-20AY\\ \\20AY=100-(1180)/(19)=(1900-1180)/(19)=(720)/(19)\\ \\AY=(36)/(19)`

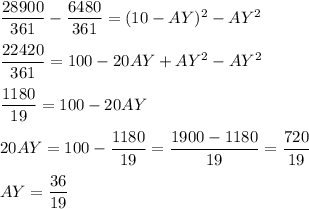
Hence,

`XY^2=(6480)/(361)-\left((36)/(19)\right)^2=(6480-1296)/(361)=(5184)/(361)\\ \\XY=(72)/(19)`