Answer:
2 quarts
Explanation:
We know that an automobile's radiator has a capacity of fifteen quarts and currently carries twelve quarts of a thirty percent antifreeze solution.
We are to find the number of quarts of pure antifreeze that must be added to strengthen the solution to forty percent.
We can write the following equation for this and solve it:
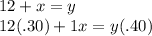
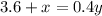
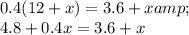
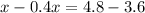
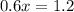

Therefore, 2 quarts are needed.