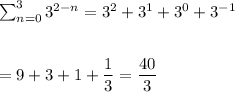Question

Wyatt claims that _ is equivalent to _ Which statement about his claim is true in every aspect?

Answer 1

D in short

Explanation:

Ed2021

Answer 2

The statement that is true in every aspect regarding his claim is:

• False, because when combined in this manner, the alternating signs of the series are lost ( Wyatt ignored the negative in the first factor)

Explanation:

The series is given as:

`\sum_(n=0)^(3) (-(1)/(3))^n\cdot 9`

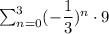
which could also be written by:

`\sum_(n=0)^(3) (-(1)/(3))^n\cdot 9=\sum_(n=0)^(3) (-(1)/(3))^n\cdot 3^2\\\\\\\sum_(n=0)^(3) (-(1)/(3))^n\cdot 9=\sum_(n=0)^(3) (-1)^n((1)/(3))^n\cdot 3^2`

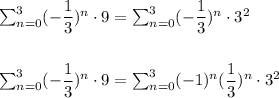
i.e.

`\sum_(n=0)^(3) (-(1)/(3))^n\cdot 9=\sum_(n=0)^(3) (-1)^n\cdot 3^(-n)\cdot 3^2\\\\\\\sum_(n=0)^(3) (-(1)/(3))^n\cdot 9=\sum_(n=0)^(3) (-1)^n\cdot 3^(2-n)`

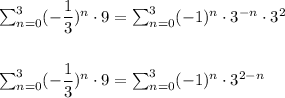
which is not equivalent to:
`\sum_(n=0)^(3) 3^(2-n)`

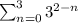
Since, on expanding the actual series we get the sum as:

`\sum_(n=0)^(3) (-(1)/(3))^n\cdot 9=(-(1)/(3))^0\cdot 9+(-(1)/(3))^1\cdot 9+(-(1)/(3))^2\cdot 9+(-(1)/(3))^3\cdot 9\\\\\\=9-(1)/(3)* 9+(1)/(3^2)* 9-(1)/(3^3)* 9\\\\\\=9-3+1-(1)/(3)\\\\\\=(22)/(3)`

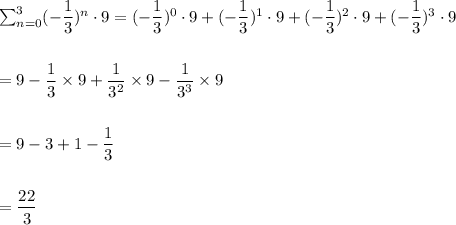
Now, the expansion of:

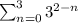`\sum_(n=0)^(3) 3^(2-n)` is:

`\sum_(n=0)^(3) 3^(2-n)=3^2+3^1+3^0+3^(-1)\\\\\\=9+3+1+(1)/(3)=(40)/(3)`