Question

A number line contains points Q, R, S, and T. Point Q is on the coordinate 24, R is on the coordinate 28, S is on the coordinate 29, T is on the coordinate 42. Find the probability that a point chosen at random on QT is on ST. Express your answer as a percent.

Answer 1

Probability = 72.2%

Explanation:

A number line contains points Q, R, S, and T with coordinated 24, 28, 29, and 42 respectively.

Now if a point lies on QT then the length of QT= coordinate of T - coordinate of Q

= 42 - 24

= 18

If a point lies on ST then the length of ST = coordinate of T - coordinate of S

= 42 - 29

= 13

Now we know Probability of an event =
`\frac{\text{Favorable event}}{\text{Total possible events}}* 100`

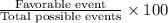
Probability =
`(13)/(18)* 100`

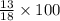
= 72.2%

Therefore, probability that a point chosen on QT will lie on ST will be 72.2%

Answer 2

72%

Explanation:

QT has length 42-24 = 18.

ST has length 42-29 = 13.

The length ST is 13/18 ≈ 72.2% of the length of QT.