Answer:
Explanation:
In order to answer all of these questions we need the position function and the acceleration function. We will discuss why when we get there.
The velocity function is given; in order to find the position function we have to take the antiderivative of the velocity function. So in order are the position, velocity, and acceleration functions below:
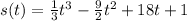
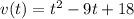
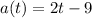
I know the constant on the position function is 1 because the info given tells me that s(0) = 1.
For the first question, the formula to find the average velocity is as follows:
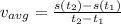
To find s(t2) and s(t1) we sub in 8 for t2 and 0 for t1 to get the following:
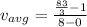
That simplifies to
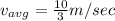
The second question wants the instantaneous velocity at t = 5. We get this by subbing in a 5 for t in the velocity function:
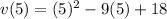 and
and
v(5) = -2. This means that the velocity of the particle is 2 m/sec, but it is now going in the opposite (or negative) direction.
The third question is asking for the time interval when the particle is moving to the right. On a velocity/time graph, the x's represent the time and the y's represent the velocity. If the "y" values are positive, then the velocity is positive and that means the object is moving to the right. Where the "y" values are negative, that means that the velocity is negative and the object is moving to the left. To find the answer to this problem we think about the positive and negative y values. Because this is a parabola, I know that the places where the graph goes through the x-axis is where the velocity changes from positive to negative and back to positive. In order to find those places where the graph goes through the x-axis I have to factor the velocity function. When I throw that into the quadratic formula on my calculator I get that x = 3 and x = 6. Completing the square on the velocity function gives me a vertex of
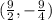
Because the y value of the vertex is negative, that means that the values of x from negative infinity to x = 3 give positive velocity values, between x = 3 and x = 6 the values of the velocity are negative, and from x = 6 to x = positive infinity the velocity is positive again.
So to sum up question 3, the particle is moving to the right on the intervals
(-∞, 3] and [6, ∞)
The fourth question is really tricky. It requires you to remember some of your Physics and how velocity and acceleration vectors are related. If the acceleration and the velocity both have the same sign, whether it be positive or negative, the object is speeding up. If the acceleration and velocity vectors have opposite signs, one positive and one negative, then the object is slowing down. We already know that from negative infinity to 3 the velocity is positive, so let's check the acceleration values in that interval. I only need to test one number, so let's test a(2).
a(2) = 2(2) - 9 and a(2) = -5
-5 means the object is slowing down here since the velocity is positive and the acceleration is negative.
Let's test the interval between 3 and 6. Let's test a(4).
a(4) = -1
Between the interval of 3 and 6 seconds, the velocity is negative. Since the acceleration is also negative, the object is speeding up between the time interval [3, 6].
We already found that from the left of t = 3, the object was slowing down; so it would also be slowing down to the right of t = 6.
Phew! That's it! We're done!