Answer:
Last option: 36,-36
Explanation:
The vertex form of the function of a parabola is:

Where (h,k) is the vertex.
To write the given function in vertex form, we need to Complete the square.
Given the Standard form:

We need to add and subtract
 on one side in order to complete the square.
on one side in order to complete the square.
Then, given
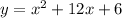 , we know that:
, we know that:
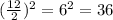
Then, completing the square, we get:
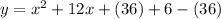
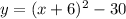 (Vertex form)
(Vertex form)
Therefore, the answer is: 36,-36