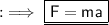Answer:
Let F be external force applied on the body in the direction of motion of the body for time interval
 , the the velocity of a body of mass m changes from
, the the velocity of a body of mass m changes from
 to
to
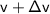 i.e. change in momentum,
i.e. change in momentum,
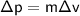 .
.
According to Newton's second law :
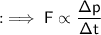

Where k is a constant of proportionality.
If limit
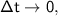 then the term
then the term
 becomes the derivative
becomes the derivative
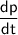 .
.
Thus,

For a body of fixed mass (m), we have :
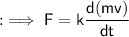
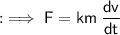
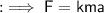
If v is fixed and m is variable then :
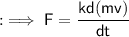
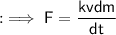
because, k = 1 then :
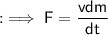
Now, a unit force may be defined as the force which produces unit acceleration in a body of unit mass :]
So,
F = 1
m = 1
a = 1
k = 1
So,