Question

Math 283 Calculus III Chapter 16 curl and divergence ​

Answer 1

Compute the curl:

`\mathrm{curl} \vec F = \left((\partial)/(\partial x) \, \vec\imath + (\partial)/(\partial y) \, \vec\jmath + (\partial)/(\partial z) \, \vec k\right) * \left(xyz\,\vec\imath + yz\,\vec\jmath + xy\,\vec k\right) \\\\ ~~~~~~~~ = \left((\partial(xy))/(\partial y)-(\partial(yz))/(\partial z)\right) \,\vec\imath + \left((\partial(xyz))/(\partial z) - (\partial(xy))/(\partial x)\right) \,\vec\jmath + \left((\partial(yz))/(\partial x) - (\partial(xyz))/(\partial y)\right) \, \vec k \\\\ ~~~~~~~~ = \boxed{(x - y) \,\vec\imath + (xy - y) \,\vec\jmath - xz\,\vec k}`

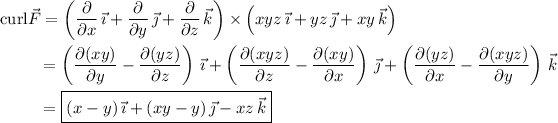
Compute the divergence:

`\mathrm{div} \vec F = (\partial(xyz))/(\partial x) + (\partial(yz))/(\partial y) + (\partial (xy))/(\partial z) = yz + z + 0 = \boxed{(y+1)z}`

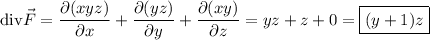
A conservative vector field has zero curl, which is not the case here, so
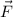`\vec F` is not conservative.

We can also employ the same method as I showed in an earlier question of yours [28193504]. We want to find a scalar function
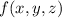`f(x,y,z)` whose gradient is
`\vec F`, so

`(\partial f)/(\partial x) = xyz \implies f(x,y,z) = \frac12 x^2yz + g(y,z)`

`(\partial f)/(\partial y) = yz = \frac12 x^2 z + (\partial g)/(\partial y)`

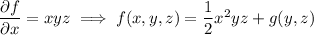
However, there is no function
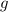`g` that depends only on
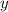`y` and
`z` that satisfies this partial differential equation; to wit, we cannot eliminate
`x`. So no such
`f` exists.