Question

scores on a college entrance examination are normally distributed with a mean of 500 and a standard deviation of 100% of people who write this exam obtain scores between 425 and 575​

Answer 1

We have

`\mu = 500`

`\sigma = 100`

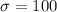
425 corresponds to a z of

`z_1 = (425 - 500)/(100) = -\frac 3 4`

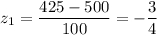
575 corresponds to

`z_2 = (575 - 500)/(100) = \frac 3 4`

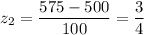
So we want the area of the standard Gaussian between -3/4 and 3/4.

We look up z in the standard normal table, the one that starts with 0 at z=0 and increases. That's the integral from 0 to z of the standard Gaussian.

For z=0.75 we get p=0.2734. So the probability, which is the integral from -3/4 to 3/4, is double that, 0.5468.

Answer: 55%