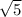Answer:
Ans 1) The correct option is B) 98.5
Ans 2) The correct option is C)
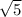
Explanation:
The angle measurement between two vectors by:
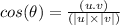
Magnitude of vector t=ai+bj, calculated by:

The given vectors are
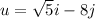 and
and
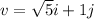
First find the dot product of u and v;

Now, Find the magnitude of both vectors u and v.
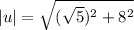
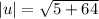
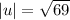
and
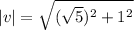
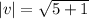
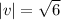
Now, put the all values in
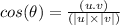
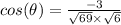

take arc cos both the sides,
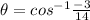
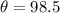 (approx)
(approx)
Therefore, the correct option is B) 98.5
Ans 2) calculate IvI by
If t= ai +bj then magnitute is
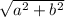
Given : v = (-2,-1)
it means v = -2i -1 j
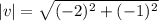
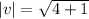
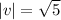
Therefore, the correct option is C)