Question

I don’t understand why is it “not possible”.

-2/3x<4 and 3/4x<-6

And also I don’t understand why is it “all real numbers”.

3x-9≤9 or 4-x≤3

Answer 1

Let's solve the inequalities: we have

`-(2)/(3)x<4 \iff -2x<12 \iff x>-6`

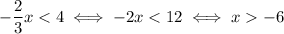
and

`(3)/(4)x<-6 \iff 3x<-24 \iff x<-8`

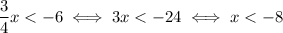
Since the two inequality must be true at the same time (there is an "and" between the two), we should find a number that is, at the same time, greater than -6, and smaller than -8. But since -6 is greater than -8, a number greater than -6 is automatically greater than -8 as well. So, it is impossible for a number to be greater than -6 and smaller than -8.

If negative numbers confuse you, this example shows the same (impossible) logic: we can't ask for a number to be greater than 10, but smaller than 3.

As for the second exercise:

`3x-9\leq 9 \iff 3x \leq 18 \iff x \leq 6`

`4-x\leq 3 \iff -x \leq -1 \iff x \geq 1`

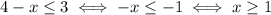
So, a number satisfies this system if it is smaller than 6 or greater than 1. This means that at least one of the conditions must be satisfied, and this is always the case:

1. If we choose a number smaller than 1, the second condition is met
2. If we choose a number between 1 and 6, both are met
3. If we choose a number greater than 6, the first condition is met

So, whatever number we choose, at least one of the conditions will be true, and the logical "OR" will be satisfied.