Question

What is the height of a student who’s z score is 3? When the mean is 49 inches and the standard deviation is 2

Answer 1

The student is 55 inches tall.

Explanation:

To solve this problem we need to use the following formula

`Z=(x- \mu)/(\sigma)`

Where
`Z` is the z-value,
`\mu` is the mean,
`\sigma` is the standard deviation and
`x` is the height of the student.

In this case, we have

`Z=3\\\mu=49\\\sigma=2`

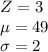
Replacing all these values, we have

`3=(x- 49)/(2)\\6=x-49\\x=6+49\\x=55`

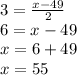
Therefore, the student is 55 inches tall.

Answer 2

55 inches

Explanation:

This question is on z-score for a sample

The general formula for finding z score for a sample is;

z=(x-μ)/δ...................where x is the sample is the height , μ is the mean and δ is the standard deviation

Given;

z=3 x=? μ=49 δ=2

Substitute values above in the general formulae

z=(x-μ)/δ

3=(x-49)/2

`3=(x-49)/(2) \\\\\\3*2=x-49\\\\\\6=x-49\\\\\\6+49=x\\\\\\55=x`