Question

A. Look at the diagram of the two squares shown below.

The Pythagorean theorem says that for any right triangle, the square of the length of the hypotenuse, c, is equal to the sum of the squares of the lengths of the legs (a and b): a2 + b2 = c2. Explain how the diagram shown above can be used to prove the Pythagorean theorem. Show your work.

B. Look at the small box shown below.

What is the length of the diagonal of the box shown? Leave your answer in radical form. Show your work and explain your steps.

Answer 1

Squares 1 and 2 have the same area because they're both (a+b) on a side.

Each of these squares is covered by four identical right triangle tiles, legs a,b, hypotenuse c.

In the first picture we see the uncovered part of the square, not covered by triangular tiles, is two squares, area
`a^2+b^2`.

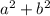In the second picture the uncovered part of the square is a smaller square, area
`c^2`.

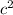We just moved the tiles around on the square, so the uncovered part is the same in both cases. So

`a^2 + b^2 = c^2`

--------

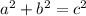
The rectangular prism has a bottom rectangular base 6 by 8. So the diagonal is
`√(6^2+8^2)=√(100)=10`.

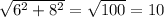The diagonal and the 7 cm side make a right triangle whose hypotenuse is the diagonal of the rectangular prism we seek.

`√(10^2 + 7^2) = √(149)`

Answer: √149