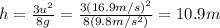Answer:
10.9 m
Step-by-step explanation:
We can solve the problem by using the law of conservation of energy.
The initial mechanical energy is just the kinetic energy of the ball:
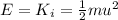
where m is the mass of the ball and u = 16.9 m/s the initial speed.
At a height of h, the total mechanical energy is sum of kinetic energy and gravitational potential energy:
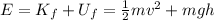
where v is the new speed, g is the gravitational acceleration, h is the height of the ball.
Due to the conservation of energy,
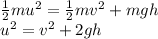 (1)
(1)
Here, at a height of h we want the speed to be 1/2 of the initial speed, so
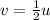
So (1) becomes
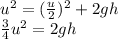
So we can find h: