Question

Solve for x: −2(x + 3) = −2x − 6

a 0
b 3
c all real numbers
d no solution

Answer 1

all real numbers

Explanation:

trust me it will pay off

Answer 2

Answer: Option C

all real numbers

Explanation:

We have the following equation

`-2(x + 3) =-2x - 6`

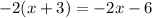
We must solve for the variable x

`-2(x + 3) =-2x - 6`

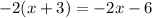
Apply the distributive property of the left side of equality

`-2*x -2*3 =-2x - 6`

`-2x -6 =-2x - 6`

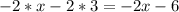
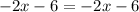
Add 6 on both sides of equality

`-2x -6 +6=-2x - 6+6`

`-2x=-2x`

Divide between -2x on both sides of the equation

`(-2x)/(-2x)=(-2x)/(-2x)`

`1=1`

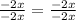
The variable x is eliminated. This means that equality does not depend on the value of x. In other words, equality is satisfied for any value of x. Therefore the equation has infinite solutions

The answer is all real numbers