Answer:
the vertex is:
(2, -1)
Explanation:
First solve the equation for the variable y
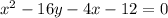
Add 16y on both sides of the equation
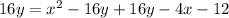
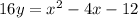
Notice that now the equation has the general form of a parabola
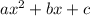
In this case
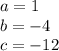
Add
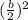 and subtract
and subtract
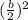 on the right side of the equation
on the right side of the equation
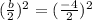
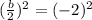
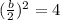
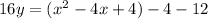
Factor the expression that is inside the parentheses

Divide both sides of the equality between 16
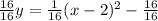
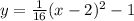
For an equation of the form
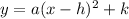
the vertex is: (h, k)
In this case
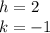
the vertex is:
(2, -1)