Question

Estimate the x-coordinates at which the relative maxima and relative minima occur for the function.

f(x) = 3x3 + 9x2 – 1

Answer 1

Relative minimum occurs at x=0

Relative maximum occurs at x=-2

Explanation:

Answer 2

Relative minimum occurs at x=0

Relative maximum occurs at x=-2

EXPLANATION

The given function is;

`f(x) = 3 {x}^(3) + 9 {x}^(2) - 1`

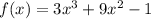
We take the first derivative to get:

`f'(x) = 9 {x}^(2) + 18x`

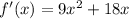
At turning point f'(x)=0

`9 {x}^(2) + 18x = 0`

`9x(x + 2) = 0`

`x = 0 \: or \: x = - 2`

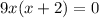
We take the second derivative to get

`f''(x) = 18x + 18</p><p>`

`f''(0) = 18(0) + 18 = 18 \: > \: 0`

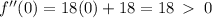
Relative minimum occurs at x=0

`f''( - 2) = 18( - 2)+ 18 = - 18 \: < \: 0`

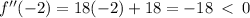
Relative maximum occurs at x=-2