ANSWER
Relative minimum occurs at x=0
Relative maximum occurs at x=-2
EXPLANATION
The given function is;
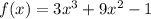
We take the first derivative to get:
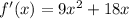
At turning point f'(x)=0
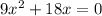
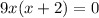
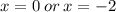
We take the second derivative to get
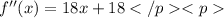
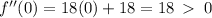
Relative minimum occurs at x=0
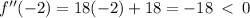
Relative maximum occurs at x=-2