Answer:
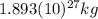
Step-by-step explanation:
This problem can be solved by the Third Kepler’s Law of Planetary motion, which states:
“The square of the orbital period of a planet is proportional to the cube of the semi-major axis (size) of its orbit”.
In other words, this law stablishes a relation between the orbital period
 of a body (moon, planet, satellite) orbiting a greater body in space with the size
of a body (moon, planet, satellite) orbiting a greater body in space with the size
 of its orbit.
of its orbit.
This Law is originally expressed as follows:
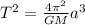 (1)
(1)
Where;
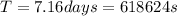 is the period of the orbit Ganymede describes around Jupiter
is the period of the orbit Ganymede describes around Jupiter
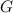 is the Gravitational Constant and its value is
is the Gravitational Constant and its value is
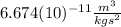
 is the mass of Jupiter (the value we need to find)
is the mass of Jupiter (the value we need to find)
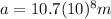 is the semimajor axis of the orbit Ganymede describes around Jupiter (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit)
is the semimajor axis of the orbit Ganymede describes around Jupiter (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit)
If we want to find
 , we have to express equation (1) as written below and substitute all the values:
, we have to express equation (1) as written below and substitute all the values:
 (2)
(2)
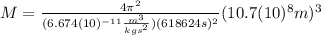 (3)
(3)
Finally:
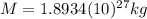 This is the mass of Jupiter
This is the mass of Jupiter