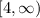Answer:
The the vertex is: (2, 4)
Domain: all real numbers
Range:
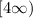
Explanation:
Quadratic functions can be written vertically as follows

Quadratic functions can be written vertically as follows
Where the point (h, k) represents the vertex of the quadratic function.
For this type of functions the domain is always all real numbers and the range is
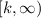 or if
or if
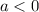 then the range is
then the range is
![(-\infty, k]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8z86pajiahfn9vqbgggbrwksuixf8rr8zz.png)
In this case the function is:
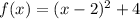
So
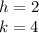
The the vertex is: (2, 4)
Domain: all real numbers
Range: